Determination of ortho- / para- hydrogen ratio using Raman spectroscopy – Application to fuel cells
January 5, 2024
Download This ApplicationIntroduction
Hydrogen is an attractive energy source for use with fuel cells. The hydrogen molecule has two different nuclear spin isomers: ortho-hydrogen (same direction pair) and para-hydrogen (opposite direction pair). Both ortho- and para-hydrogen exhibit the same chemical properties, whilst their physical properties, such as the specific heat are different from each other, and since the conversion between the ortho- and para- isomers requires an extremely long time, each molecule tends to be handled as different from the other. The abundance ratio of ortho-to para- in hydrogen gas at ambient temperature is stable at approx. 3:1, but when it is cooled to a liquid, most hydrogen molecules convert to para-hydrogen. However, a portion of the ortho-hydrogen also becomes a liquid, and the ortho- to para- isomer conversion in liquid hydrogen after an extended time may generate heat, which can affect the storage efficiency. Therefore, when hydrogen gas is liquefied for industrial purposes, an ortho- to para- conversion catalyst is necessary. Using Raman spectroscopy (NRS-5000) for this experiment, we will describe a simple evaluation of the ortho-/para- abundance ratio .
Experimental
An NRS-3100 (or NRS-5100) Laser Raman spectrophotometer was used for the measurement. A 10 cm FT-IR gas cell with NaCl windows was evacuated using a vacuum pump, and then hydrogen gas with a pressure lower than one atmosphere was filled directly into the gas cell from an H2 gas cylinder. The gas cell is mounted as shown in Figure 1, and the measurement was performed using a long working distance objective lens by focusing the beam inside the cell (Excitation wavelength; 532 nm, laser power at sample point is approximately 10 mW).
Keywords
230-AN-0006
Results
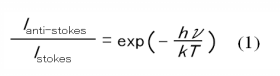Figure 2 illustrates the Raman spectrum obtained for the hydrogen gas. The peaks due to the rotational transitions were seen in the spectrum in the range from 350 to 1100 cm-1. The system temperature was estimated from the Stokes/anti-Stokes ratio using equation (1) to be approximately 300K.
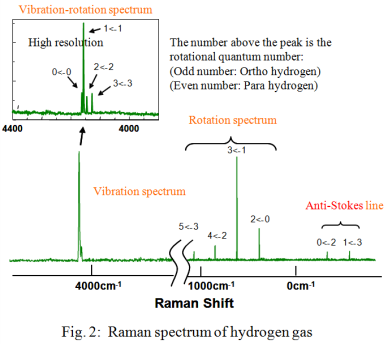
The ortho-para abundance ratio is calculated from each partition function equation (2) of the ortho- and para-hydrogen isomers by adding the peak height of the ortho- and para-hydrogen peaks in the rotation spectrum and using the estimated temperature of 300K in equation (2); the ratio of 7:3 was obtained from the calculations. The hydrogen molecular rotation constant B in equation (2) was referred to B=59 cm-1 which was calculated from the equal distance of the rotation line 4B.
Compared to the standard ortho-para ratio of hydrogen at an ambient temperature of 3:1, the ratio of para hydrogen is higher in the experimental example. From this result, it is noted that some of the ortho-hydrogen was already converted to para-hydrogen when hydrogen in the cylinder was liquefied and the cylinder filled. In this example, the ortho-para ratio was obtained from the rotation spectrum, but, when the Raman spectrum in the vicinity of the peaks of the rotation spectrum is affected by extraneous light, e.g., fluorescence generated from the window, the abundance ratio can also be calculated from the vibration-rotation spectrum which is separated from the rotational spectrum peaks by using a high resolution measurement of the vibration-rotation spectrum around 4160 cm-1.
Conclusion
The reason why the difference in the direction of nuclear spin for molecules such as ortho- and para-hydrogen is evaluated by Raman spectroscopy (vibration spectroscopy) can be explained by quantum-mechanics. The wave function of the whole hydrogen molecule can be expressed as the product of the separate wave functions for the electronic, vibrational, rotational energies and the nuclear spin as shown in equation (3).
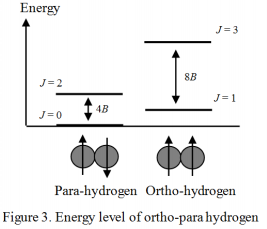
Equations (4) and (5) show the energy of the molecular vibration and rotation, respectively, calculated from the characteristic values of the Schrödinger equation.
Figure 3. shows the energy level of the hydrogen molecule using a quantum number of rotation J. Generally, in the electronic ground state, the wave function of the electronic and vibrational quanta is symmetric to the displacement of the nucleus. On the other hand, the wave function of the nuclear spin has both symmetric and asymmetric cases to the displacement, and in each case is called ortho- and para-. The wave function of rotation must be symmetric in order to satisfy the Pauli exclusion principle. Therefore, ortho-hydrogen exists only when the rotation level J is odd (asymmetric), and para-hydrogen exists only when the rotation level J is even (symmetric). The nuclear spin information such as that for ortho- and para-hydrogen can be obtained from the rotation spectrum (or vibration-rotation spectrum) of the hydrogen molecule. However, in the case of a Deuterium molecule (D2), the Deuterium atom is a Bose particle, so that the relationship between odd – even and ortho – para is contrary to the hydrogen molecular case, with the resulting interesting phenomenon that the shape of the rotation spectrum dramatically changes.
Featured Products:
Determination of ortho- / para- hydrogen ratio using Raman spectroscopy – Application to fuel cells
Introduction
Hydrogen is an attractive energy source for use with fuel cells. The hydrogen molecule has two different nuclear spin isomers: ortho-hydrogen (same direction pair) and para-hydrogen (opposite direction pair). Both ortho- and para-hydrogen exhibit the same chemical properties, whilst their physical properties, such as the specific heat are different from each other, and since the conversion between the ortho- and para- isomers requires an extremely long time, each molecule tends to be handled as different from the other. The abundance ratio of ortho-to para- in hydrogen gas at ambient temperature is stable at approx. 3:1, but when it is cooled to a liquid, most hydrogen molecules convert to para-hydrogen. However, a portion of the ortho-hydrogen also becomes a liquid, and the ortho- to para- isomer conversion in liquid hydrogen after an extended time may generate heat, which can affect the storage efficiency. Therefore, when hydrogen gas is liquefied for industrial purposes, an ortho- to para- conversion catalyst is necessary. Using Raman spectroscopy (NRS-5000) for this experiment, we will describe a simple evaluation of the ortho-/para- abundance ratio .
Experimental
An NRS-3100 (or NRS-5100) Laser Raman spectrophotometer was used for the measurement. A 10 cm FT-IR gas cell with NaCl windows was evacuated using a vacuum pump, and then hydrogen gas with a pressure lower than one atmosphere was filled directly into the gas cell from an H2 gas cylinder. The gas cell is mounted as shown in Figure 1, and the measurement was performed using a long working distance objective lens by focusing the beam inside the cell (Excitation wavelength; 532 nm, laser power at sample point is approximately 10 mW).
Results
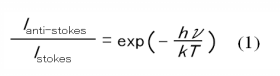Figure 2 illustrates the Raman spectrum obtained for the hydrogen gas. The peaks due to the rotational transitions were seen in the spectrum in the range from 350 to 1100 cm-1. The system temperature was estimated from the Stokes/anti-Stokes ratio using equation (1) to be approximately 300K.
The ortho-para abundance ratio is calculated from each partition function equation (2) of the ortho- and para-hydrogen isomers by adding the peak height of the ortho- and para-hydrogen peaks in the rotation spectrum and using the estimated temperature of 300K in equation (2); the ratio of 7:3 was obtained from the calculations. The hydrogen molecular rotation constant B in equation (2) was referred to B=59 cm-1 which was calculated from the equal distance of the rotation line 4B.
Compared to the standard ortho-para ratio of hydrogen at an ambient temperature of 3:1, the ratio of para hydrogen is higher in the experimental example. From this result, it is noted that some of the ortho-hydrogen was already converted to para-hydrogen when hydrogen in the cylinder was liquefied and the cylinder filled. In this example, the ortho-para ratio was obtained from the rotation spectrum, but, when the Raman spectrum in the vicinity of the peaks of the rotation spectrum is affected by extraneous light, e.g., fluorescence generated from the window, the abundance ratio can also be calculated from the vibration-rotation spectrum which is separated from the rotational spectrum peaks by using a high resolution measurement of the vibration-rotation spectrum around 4160 cm-1.
Conclusion
The reason why the difference in the direction of nuclear spin for molecules such as ortho- and para-hydrogen is evaluated by Raman spectroscopy (vibration spectroscopy) can be explained by quantum-mechanics. The wave function of the whole hydrogen molecule can be expressed as the product of the separate wave functions for the electronic, vibrational, rotational energies and the nuclear spin as shown in equation (3).
Equations (4) and (5) show the energy of the molecular vibration and rotation, respectively, calculated from the characteristic values of the Schrödinger equation.
Figure 3. shows the energy level of the hydrogen molecule using a quantum number of rotation J. Generally, in the electronic ground state, the wave function of the electronic and vibrational quanta is symmetric to the displacement of the nucleus. On the other hand, the wave function of the nuclear spin has both symmetric and asymmetric cases to the displacement, and in each case is called ortho- and para-. The wave function of rotation must be symmetric in order to satisfy the Pauli exclusion principle. Therefore, ortho-hydrogen exists only when the rotation level J is odd (asymmetric), and para-hydrogen exists only when the rotation level J is even (symmetric). The nuclear spin information such as that for ortho- and para-hydrogen can be obtained from the rotation spectrum (or vibration-rotation spectrum) of the hydrogen molecule. However, in the case of a Deuterium molecule (D2), the Deuterium atom is a Bose particle, so that the relationship between odd – even and ortho – para is contrary to the hydrogen molecular case, with the resulting interesting phenomenon that the shape of the rotation spectrum dramatically changes.
Keywords
230-AN-0006